미분
미분은 기울기이다. 신기하게도 x값에 미분값을 더하여 이동하면 f(x)값은 증가하고 미분값을 빼면 f(x)값은 감소한다.
f'(x)가 음수 라면 아래 그림처럼 x는 왼쪽으로 이동하므로 f(x+f'(x)) > f(x)가 된다. (반대로 f'(x)값을 빼면 오른쪽으로 감소소하는 방향으로 간다.)
f'(x)가 양수라면 우상향 그래프가 될테고 f'(x)만큼 오른쪽으로 이동하니 f(x+f'(x)) > f(x)가 성립한다.
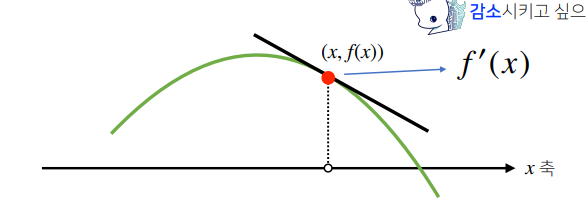
미분 더하기 : f(x+f'(x)) >> 값 증가 (미분 더하기)
미분 빼기 : f(x-f'(x)) >> 값 감소
극소값 / 극대값 구하기 및 경사하강법
위 성질을 이용해서 f(x+f'(x))를 계속 하거나 f(x-f'(x))를 계속 할 경우 f'(x)=0이되는 극소, 극대점에서 결국 정지하게된다.
이를 이용해 코드로 작성하면 아래와 같다.
여기서 abs(grad)는 f'(x)값의 절대 값으로 원래는 이게 0일 때 정지해야하다 컴퓨터로 계산 할 때 정확히 0이되기 불가능하므로 eps를 설정하여 eps보다 기울기가 작을 경우 극점으로 해석하여 정지한다.
grad 는 f'(x)이고 var = var = lr * grad 는 x - lr*f'(x)이다. lr 을 통해 학습속도를 조절 할 수 있다.

변수가 벡터일 경우
변수가 벡터일 경우 각 변수 별로 편미분을 해준 그레디언트 벡터 를 이용한다. (각 변수별 기울기들의 벡터 같은 느낌이다)
ex) f(x, y) = x^2 +2y^2 는 (x^2, 2y^2)벡터로 표현하고 이를 편미분하면 (2x, 4y) 벡터가된다.
그레디언트 벡터는 아래 그림의 검은 화살표다.

이를 코드로 표현 할 때 그레디언트 벡터가 grad가 된다. 하지만 그레디언트 벡터의 절대값을 이용하지 않고 norm을 사용하여 벡터의 길이를 통해 종료조건을 설정한다. (결국 비슷한 의미인거 같다.)

경사하강법으로 선형회귀 계수 β 구하기
Xβ와 Y들의 L2노름이 최소화하는 β를 찾아야된다. 앞에서는 무어 펜로즈를 이용했지만 여기선 경사하강법을 이용한다.
윗줄의 밑줄친 부분을 표현하면 Y - Xβ의 L2노름의 최소 값이다.


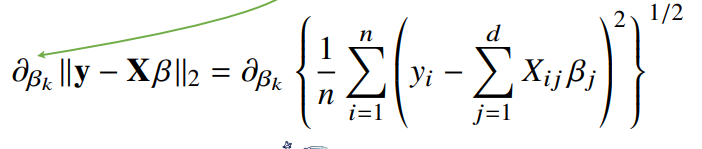

식들을 정리하면 위와 같이된다. XT는 X의 전치 행렬이다.
따라서 코드로 구현 할때 X를 전치 시키는 transpose(X)를 이용한다.
||Y-Xβ||2 를 최소화 하는 β이므로 gradient를 빼줘야된다.
gradient는 위 그림들을 통해서 XT * (y-Xβ) 즉 transpose(x) @ error로 표현한다.

경사 하강법은 만능일까
이론적으로 경사하강법은 미분 가능하고 볼록한 함수에 대해선 수렴이 보장된다.ㅜ
하지만 비선형회귀의 문제의 경우 목적식이 볼록하지 않을 수 있다.

확률적 경사하강법
데이터중 한개 또는 일부만을 이용하여 업데이트한다. 볼록이 아닌 목적식도 SGD를 통해 최적화할 수 있다.
위의 밑줄친 부분은 즉 미니 배치를 이용하여 그레디언트 벡터를 계산하는것이다. 이로 인해 다소 부정확 할 수 있지만 계산 속도가 훨씬 빠르다. 따라서 같은 시간에 더 많은 step을 나아갈 수 있다.
'기타 > 리뷰 및 경험담 - p stage' 카테고리의 다른 글
| [AI Math] 딥러닝 학습 방법 (0) | 2021.09.23 |
|---|---|
| [AI Math] 벡터와 행렬 (0) | 2021.09.22 |
| [부스트캠프] (1주차) 필수 과제 1~5 관련 정리 (0) | 2021.08.06 |

